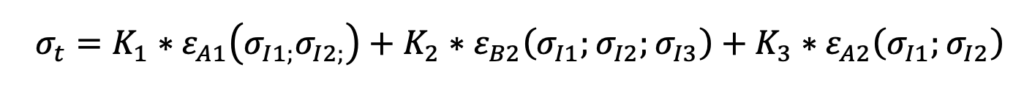Dritti al cuore delle tensioni con il ring core


Il metodo ring core sta trovando affermazione nell’ambito della misurazione delle tensioni residue. Pur soffrendo della mancanza di una normativa standard, tale metodo è stato scelto e adottato da realtà blasonate. Un colosso come Siemens, per esempio, ne ha fatto una specifica modalità esecutiva richiesta ai propri fornitori. Approfondiamo le peculiarità di questa nuova impostazione metodologica, descrivendone le modalità esecutive e mettendone in luce l’importanza ogni qual volta si desidera conoscere gli stati tensionali più interni del materiale, eliminando il “disturbo” costituito dalle alterazioni superficiali.
Il perché di un successo
il metodo hole drill secondo normativa ASTM E-837/20 si applica fino alla profondità di 1 mm, con la possibilità di arrivare fino a 2mm quando ci interessi solo quantificare l’energia di deformazione complessivamente immagazzinata.
Una profondità sicuramente significativa per un prodotto finito, visto che il 90% del comportamento in servizio di un componente dipende dallo stato della sua superficie, interfaccia tra il materiale e le sollecitazioni che provengono dal mondo circostante: del resto il premio Nobel per la fisica Wolfang Pauli disse che Dio ha creato la materia, ma il Diavolo le superfici…
Il comportamento a fatica, la resistenza alla corrosione, la resistenza all’usura sono solo alcune delle caratteristiche rispetto alle quali è solo la superficie a guidare il comportamento di un componente.
Ma se parliamo invece di un grezzo o di un semilavorato, concentrare la propria attenzione alla superficie rischia di essere fuorviante: infatti in questi stadi di lavorazione quello che effettivamente interessa sono le tensioni residue immagazzinate sotto forma di energia elastica nell’interno del materiale, energia elastica destinata ad essere liberata sotto forma di deformazione dalle successive operazioni di lavorazione meccanica o termica: in questi casi l’unica informazione che si ricava da una misurazione mediante la tecnica hole drill riguarda la bontà con cui sono state eseguite le operazioni di sgrossatura (e per esperienza, di solito sono eseguite talmente “male” che i componenti sembrano tutti pronti più per la rottamazione che per le successive lavorazioni!).
Senza dimenticarsi che quando parliamo di sbozzati di forgiatura o di fusione, molto spesso le superfici presentano crepe e fessurazioni tali da richiedere profonde asportazioni di materiale per ottenere una superficie adeguata alla applicazione degli estensimetri (fig 1).


Fig 1
Nel caso di forgiati o di fusioni in ghisa, molto spesso la finitura superficiale è tale da non rendere
possibile l’applicazione degli estensimetri (fig 1a) se non dopo una profonda alterazione della
superficie stessa (fig 1b)
In questo contesto si è sviluppato un Ring Core “di seconda generazione” che permette di estendere le osservazioni fino al cuore del materiale “filtrando” gli effetti delle alterazioni superficiali.
Ma prima di passare alla pratica, serve un po’ di teoria…
Un breve richiamo alla meccanica del continuo
Per arrivare a comprendere queste nuove modalità esecutive del ring core (ma soprattutto i modelli di calcolo per interpretarne i risultati), è necessario un breve richiamo ad alcuni concetti di meccanica del continuo, ossia quella branca della fisica che si occupa di studiare (anche) la correlazione tra le sollecitazioni applicate e le conseguenti deformazioni in un sistema che sia:
- Deformabile: cioè che sotto l’azione di forze possa cambiare forma e/o volume;
- Omogeneo: cioè che il materiale che costituisce il corpo abbia identiche proprietà in ogni sua parte;
- Isotropo: cioè che il materiale di cui è composto il corpo presenti stesse caratteristiche meccaniche in ogni direzione.
Supponiamo di avere un tale materiale sottoposto ad uno stato tensionale di trazione in campo elastico, e di ricavare su di esso una cava di profondità X (fig. 2a), liberando una porzione di materiale che indicheremo con “A”: ovviamente questa asportazione darà modo al materiale circostante di rilassarsi.
Se il nostro materiale fosse come una torta millefoglie, dove ogni strato può “scivolare” su quello sottostante, allora tale rilassamento sarebbe completo (fig. 2b): ma “purtroppo” nei materiali reali esistono i vincoli di taglio, per cui il materiale non interessato al taglio vincola il materiale sovrastante che potrà deformarsi solo parzialmente, ossia solo fino a quando l’energia elastica liberata dal taglio non eguaglia l’energia elastica derivante dal vincolo di taglio: pertanto sulla superficie potrà essere misurata una deformazione pari a e1, proporzionale ma non equivalente alla tensione residua precedentemente immagazzinata in questo primo strato di materiale (fig. 2c).
Ricavando una duplice cava in un materiale tensionato (fig 2a) , in assenza di vincoli di taglio il
rilassamento della porzione di materiale “A” separata sarebbe completa (fig 2b) , ma nella realtà
questo non avviene (fig 2c), con una deformazione E1 corrispondente solo ad una frazione
dell’energia elastica immagazzinata nel volume del materiale “A”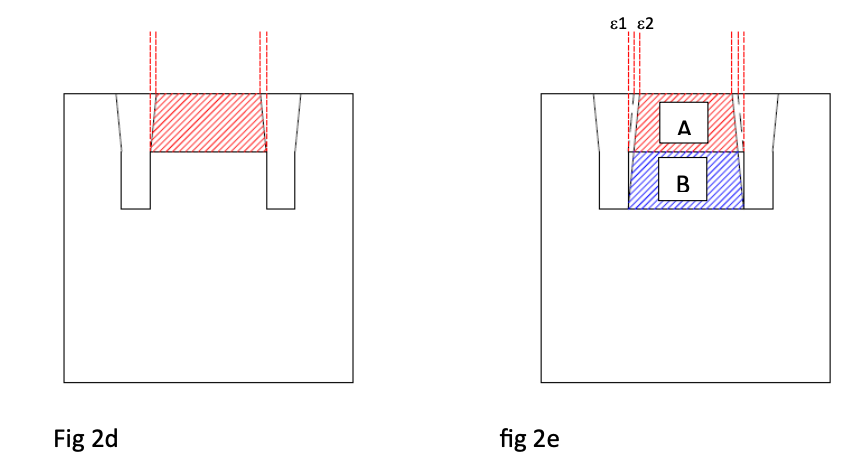
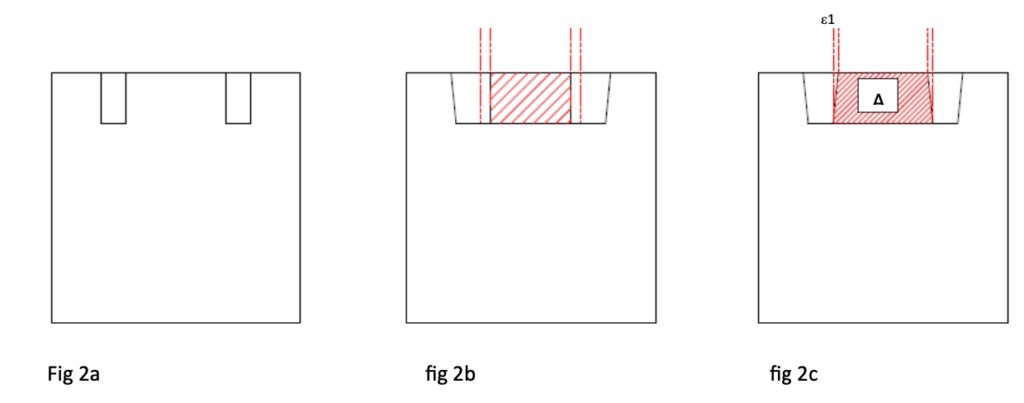
Incrementando la profondità della cava (fig 2d) , una seconda porzione di materiale “B” ha la
possibilità di rilassarsi con una deformazione rilasciata pari a E2, trascinando nel suo movimento
“geometrico” anche la porzione “A” : sulla superficie si avrebbe quindi una deformazione pari a E1
+ E2
Se raddoppiamo la profondità della cava avremo poi che la nuova porzione di materiale (indicata con “B”) interessata dalla cava a sua volta potrà rilassarsi parzialmente per una deformazione pari a e2, “trascinando” con se la porzione di materiale sovrastante per una analoga deformazione (fig. 2d).
Ma in realtà questa nuova deformazione comporta anche un altro effetto, in quanto sempre per effetto dei meccanismi di vincolo a taglio il rilassamento indotto sulla parte sottostante del materiale “libera” ulteriormente la parte sovrastante, che quindi farà registrare un ulteriore rilassamento e3.
Pertanto dopo che sono state ricavate in sequenza le cave Z1 e Z2 , in superficie è possibile rilevare una deformazione totale et pari a:
et = eA1 + eB2 + eA2
Dove
eA1 = rilassamento indotto dall’effetto della cava Z1 sulla porzione di materiale A;
eB2 = rilassamento indotto dall’ effetto geometrico del rilassamento della porzione di materiale B a seguito della realizzazione della cava Z2;
eA2 = rilassamento indotto per effetto di taglio dal rilassamento della porzione di materiale B sulla porzione di materiale A.
In realtà l’interazione tra la porzione di materiale A e la porzione di materiale B è duplice, nel senso che a sua volta A impone un vincolo di taglio su B, che pertanto vede la sua deformazione limitata sia dall’effetto della porzione di materiale A sia dall’effetto della porzione di materiale C.
In definitiva, indicando con:
- et = deformazione complessivamente rilasciata in superficie
- st = stato tensionale ricostruito a partire dalla deformazione rilasciata in superficie
- eA1= deformazione rilasciata in superficie dal volume di materiale A a seguito della esecuzione della cava z1,
- er B2= deformazione rilasciata in superficie dal volume di materiale B a seguito della esecuzione della cava z2,
- er A2= deformazione rilasciata in superficie dal volume di materiale A a seguito della esecuzione della cava z2,
- si 1= tensione residua immagazzinata nel volume di materiale A
- si 2= tensione residua immagazzinata nel volume di materiale B
- si 3= tensione residua immagazzinata nel volume di materiale C non interessato dalla cava
Tutto questo preambolo è per rendere chiaro come i rilassamenti che si possono in misurare in superficie a seguito della realizzazione di cave progressivamente più profonde non possono essere assolutamente attribuiti unicamente alla porzione di materiale asportata in quella fase, ma sono in relazione anche con gli stati tensionali degli strati di materiale immediatamente sottostante.
La procedura operativa
Come detto, nel caso di grezzi o semilavorati l’interesse ingegneristico è per gli stati tensionali presenti non sulla superficie ma nel cuore nel materiale, sia perché la superficie finisce per essere influenzata dai processi di finitura e lavorazione, sia perché la superficie corrisponde a quella parte di materiale destinata ad essere asportata o comunque alterata dalle successive fasi di lavorazione.
Da qui nasce l’intuizione di una applicazione del ring core in due step, eliminando dal calcolo la deformazione rilevata dopo il primo step e utilizzando per l’elaborazione finale solo la deformazione rilasciata nel secondo step.
Seguendo questo approccio, una procedura ottimizzata per svolgere una corretta misurazione è la seguente:
- Preparazione della superficie per l’incollaggio dello strain gauge.
È opportuno anticipare tale operazione in quanto l’ingombro del macchinario per l’esecuzione della cava anulare interferisce con l’utilizzo delle mole abrasive.
A differenza di quanto viene raccomandato nel caso ad esempio delle misurazioni con la tecnica Hole Drill, in questo caso è possibile utilizzare anche delle procedure molto aggressive, senza preoccuparsi di alterare la superficie: questo proprio perché le misurazioni relative a tale porzione di materiale saranno poi scartate .

Fig 3 dopo un opportuna preparazione della superficie finalizzata ad una corretta applicazione
dell’estensimetro, si procede alla realizzazione della cava iniziale.
- Esecuzione di una prima cava alla profondità Z1 (tipicamente 2mm) (fig. 3)
- Applicazione dell’estensimetro e azzeramento del sistema di acquisizione e condizionamento (fig. 4)
- Rimozione dei cablaggi (fig. 5) ed esecuzione del secondo step di foratura fino alla profondità finale Z2 (tipicamente 4 mm) fig. 6
- Collegamento dei cablaggi (fig. 7) e misurazione della deformazione conseguente al secondo step di foratura (fig. 8)
Per poi arrivare ad una formula risolutiva del tipo:
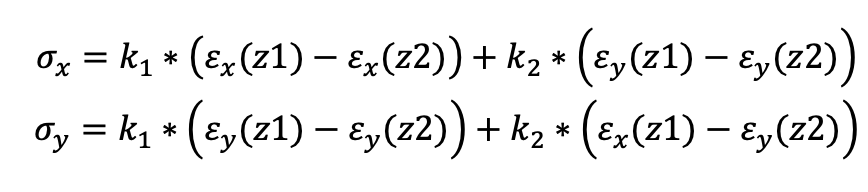

Fig 4 successivamente alla realizzazione della cava iniziale, si procede alla installazione dello strain
gauge. Fondamentale in questa fase l’allineamento delle griglie dell’estensimetro con le direzioni
longitudinale (x) e circonferenziale (y) dell’albero (dettaglio)
Fig 5 Una volta completato l’azzeramento del sistema, si procede alla rimozione dei cablaggi e alla
preparazione per il completamento della cava alla sua profondità finale.
Fig 6 completamento della cava alla sua profondità definitiva
In questa fase si consiglia la rimozione di tutti i cablaggi esterno per evitare che gli sfridi di foratura
finiscano per attorcigliarsi su di essi e danneggiarli.
Fig 7 : al termine delle operazioni di asportazione si procede al collegamento dello strain gauge per
la misurazione della deformazione rilasciata durante questo secondo step di foratura.
Dalla misura al risultato: il vero valore aggiunto
Come è facile capire, il cuore della procedura sono i coefficienti k1 e k2 , ed è proprio su questi che alla fine si differenziano le procedure Siemens, Mitsubishi Larsen e tutte le altre derivate.
Coefficienti che si differenziano non solo in funzione del tipo di estensimetro utilizzato, del diametro della cava o della sua profondità (parametri che come avremo modo di vedere alla fine possono essere gestiti con relativa facilità), ma soprattutto in base al modello interpretativo che viene adottato per modellizzare la distribuzione delle tensioni residue.
Premettiamo subito che la soluzione apparentemente più scontata, ossia quella di scartare “brutalmente” le deformazioni nel primo step e considerare unicamente il rilascio nel secondo step non è esattamente la migliore…
Consideriamo infatti la equazione 1 precedentemente ricavata:
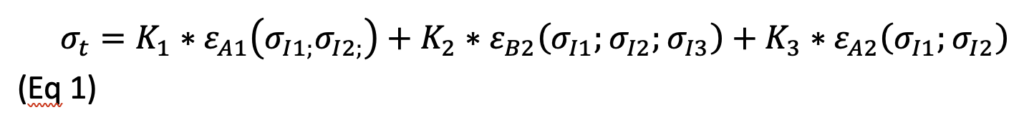
Ricordando come:
- st = stato tensionale ricostruito a partire dalla deformazione rilasciata in superficie
- eA1= deformazione rilasciata in superficie dal volume di materiale A a seguito della esecuzione della cava z1,
- er B2= deformazione rilasciata in superficie dal volume di materiale B a seguito della esecuzione della cava z2,
- er A2= deformazione rilasciata in superficie dal volume di materiale A a seguito della esecuzione della cava z2,
- si 1= tensione residua immagazzinata nel volume di materiale A
- si 2= tensione residua immagazzinata nel volume di materiale B
- si 3= tensione residua immagazzinata nel volume di materiale C non interessato dalla cava
Imponendo K1= 0 azzeriamo il contributo della deformazione rilasciata nel primo step, ottenendo la eq. 2:
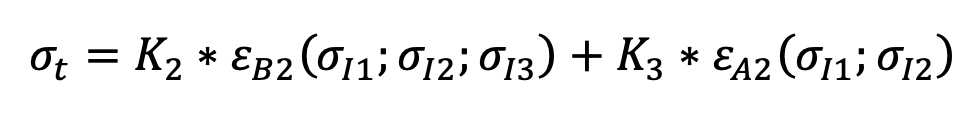
È evidente che il contributo della energia si1 immagazzinata nella porzione di materiale interessata al primo step di asportazione permane e non può semplicemente essere “dimenticata” , soprattutto in quanto tutta la teoria elaborata in accompagnamento alla tecnica hole drill ci ha insegnato che nella deformazione progressivamente rilasciata all’aumentare della profondità di asportazione il contributo degli strati superficiali rimane comunque dominate: e nella prossima pubblicazione andremo a vedere proprio come tale contributo deve essere considerato.

Fig 8 lettura del valore della deformazione differenziale intercorsa tra lo step 1 e lo step 2 di
foratura
L'articolo Dritti al cuore delle tensioni con il ring core sembra essere il primo su Meccanica News.
Qual è la tua reazione?
 Mi piace
0
Mi piace
0
 Antipatico
0
Antipatico
0
 Lo amo
0
Lo amo
0
 Comico
0
Comico
0
 Furioso
0
Furioso
0
 Triste
0
Triste
0
 Wow
0
Wow
0



















































































































































































_(54)-1765966536088.jpg--polenta__spezzatino_e_solidarieta__a_cossano_belbo__alla_cena_della_protezione_civile__consegnata_una_nuova_borsa_medica.jpg?1765966536232#)









-1754133631392.png--valerio_minato_svela_il_volto_in_movimento_del_monviso_sotto_le_stelle.png?1754133631616#)